Уравнения движения жидкости

В гидродинамике и динамической метеорологии — система дифференциальных уравнений, представляющих собой приложение второго закона Ньютона к жидкости (воздуху). Полное ускорение частицы приравнивается сумме сил, действующих на частицу. У. Д. Ж. на вращающейся Земле в векторной форме сводятся к уравнению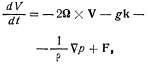

где F — сила трения на единицу массы, а остальные обозначения см. в начале словаря. В системе декартовых координат с началом в произвольной точке земной поверхности, причем оси x и y лежат в плоскости горизонта и направлены к востоку и северу, а ось z — вверх, У. Д. Ж. имеют вид:

В правых частях уравнений стоят составляющие сил Кориолиса, барического градиента, трения и тяжести. В уравнении по оси z можно пренебречь вертикальной составляющей силы Кориолиса, вертикальным ускорением и силой трения; при этих упрощениях уравнение по оси ζ принимает вид основного уравнения статики атмосферы.

Синонимы: уравнения гидродинамики, полные уравнения.